Explanation

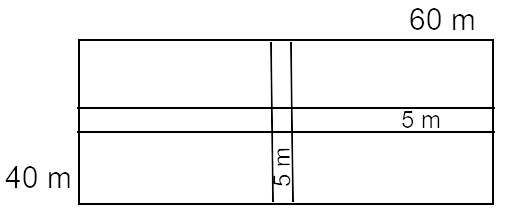
Here, length of the garden is 60 m.
Breadth of the garden is 40 m.
\therefore Area of the rectangular garden is = \left(length\ \times\ breadth\right)
=\ \left(60\ m\ \times\ 40\ m\right)
=\ 2400\ sqm
Now, the garden has two ‘5m’ wide path.
\therefore one path length is 60 m & breadth is 5 m _{[garden length = road length]}
\therefore Area of one path is = \left(60\ \times\ 5\right) sqm
= 300 sqm
And, another path length is 40 m & breadth is 5 m _{[garden breadth = road length]}
\therefore Area of another path is = \left(40\ \times\ 5\right) sqm
= 200 sqm
Here, two paths overlap one place and create a square, so we need to subtract that square value of the total area of the path.
We know, area of a square = \left(side\ \times\ side\right)
\therefore subtracting area of the path is = \left(5\ \times\ 5\right) sqm
= 25 sqm.
\therefore Total area of the path is = (sum of two path area – subtracting path area)
= \{\left(300\ +\ 200\right)\ -\ 25\} sqm
= \left(500\ -\ 25\right) sqm
= 475 sqm
According to the question,
1 sqm path paving cost = 80 rupees
\therefore 475 sqm path paving cost = \left(80\ \times475\right) rupees
= 38000 rupees.
Other side,
Area of the garden without path is = \left(2400\ -\ 475\right) sqm
= 1925 sqm.
\therefore The area of each part of the land is = \left(\frac{without\ path\ garden\ area}{4}\right) sqm
= \left(\frac{1925}{4}\right) sqm
= 481.25 sqm
Ans: The cost of paving the path is 38000 rupees & The area of each part of the land is 481.25 sqm